ความแตกต่างหลัก: เรเดียนและองศาเป็นสองหน่วยที่แตกต่างกันสำหรับการวัดมุม การศึกษาระดับปริญญาเป็นวิธีที่เก่ากว่าของการวัดมุมโดยย้อนหลังไปถึงสมัยก่อน เรเดียนเป็นวิธีการวัดมุมที่มีประสิทธิภาพมากกว่าแม้ว่าจะซับซ้อนกว่าเล็กน้อย ในความเป็นจริงแล้วหน่วย SI สำหรับการวัดมุมแม้จะใช้องศามากกว่าปกติก็ตาม

เรเดียนและองศาเป็นหน่วยต่างกันสองหน่วยสำหรับการวัดมุม สิ่งแรกที่นักเรียนคณิตศาสตร์เรียนรู้คือการวัดมุมไม่ว่าจะเป็นมุม 45 องศามุม 90 องศาเป็นต้น นักเรียนได้รับการสอนอย่างมีประสิทธิภาพว่ามุมนั้นมีความหมายเหมือนองศา อย่างไรก็ตามเป็นการศึกษาล่วงหน้าที่เราเรียนรู้เกี่ยวกับเรเดียน
เรเดียนเป็นวิธีการวัดมุมที่มีประสิทธิภาพมากกว่าแม้ว่าจะซับซ้อนกว่าเล็กน้อย ในความเป็นจริงแล้วหน่วย SI สำหรับการวัดมุมแม้จะใช้องศามากกว่าปกติก็ตาม
การศึกษาระดับปริญญาเป็นวิธีที่เก่ากว่าของการวัดมุมโดยย้อนหลังไปถึงสมัยก่อน แต่ละระดับแสดงถึง 1/360 ของการหมุนเต็ม ซึ่งหมายความว่าแต่ละวงกลมแบ่งออกเป็น 360 องศาและการเคลื่อนไหวแต่ละครั้งจะถูกนับเป็น 1 ° ดังนั้นถ้าเราย้าย 5 ครั้งจากจุดเริ่มต้น 0 องศามันก็คือห้าองศาหรือ 10 °จากนั้น 15 °และต่อไปจนกว่าเราจะกลับมาที่ 0 ทำให้เต็ม 360 °รอบวงกลม
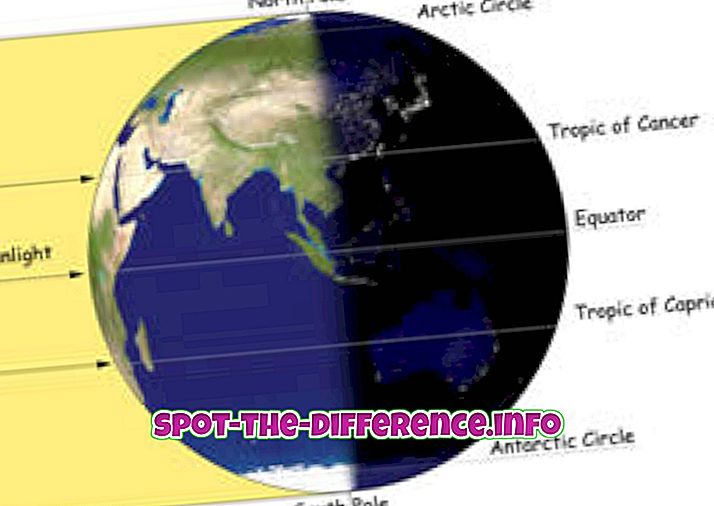
เหตุผลที่แท้จริงของสมัยก่อนแบ่งวงกลมออกเป็น 360 องศาไม่แน่ใจ แต่ทฤษฎีที่เด่นชัดระบุว่าคนโบราณเชื่อว่าปีที่สร้างขึ้นจาก 360 วันคือ 12 เดือน 30 วันในแต่ละวันและดวงอาทิตย์เคลื่อนตัวเล็กน้อย เส้นขอบฟ้าจากที่เป็นวันก่อนหน้าคือ 1 ° อีกทั้ง 360 องศาทำให้การแบ่งวงกลมค่อนข้างง่าย ดังนั้นครึ่งวงกลมของมันที่ 180 °, หนึ่งในสี่วงกลมคือ 90 °, จากนั้น 45 °, และอื่น ๆ
อย่างไรก็ตามระบบนี้ค่อนข้าง จำกัด ประการแรกระบบ 360 °แปลได้ไม่ดีนักในการคำนวณทางคณิตศาสตร์อื่น ๆ ส่วนใหญ่เนื่องจากไม่ได้ใช้ระบบ 360 ดังนั้นเรเดียนก็เข้ามาเล่น เรเดียนถูกนำมาใช้ตั้งแต่นานมาแล้วจนถึงยุค 1400 อย่างไรก็ตามมันไม่ได้ถูกนำมาใช้เป็นหน่วยที่ยอมรับจนถึงปลายปี 1800

มันใช้เวลา 3 เรเดียนในการก่อตัวเกือบครึ่งหนึ่งของวงกลม อย่างไรก็ตามแม้หลังจาก 3 เรเดียนมีเส้นรอบวงเล็กน้อยเหลืออยู่ ดังนั้นการวัดอย่างเป็นทางการคือครึ่งวงกลมเท่ากับ 3.14 เรเดียนหรือ 3.14 rad โดยทั่วไปจะเขียนเป็นπ rad หรือπr ดังนั้นหนึ่งวงกลมเท่ากับ2πr
ตั้งแต่หนึ่งวงกลมเท่ากับ2πrและเรารู้ว่าวงกลมหนึ่งเท่ากับ 360 ° ดังนั้นสามารถเขียนได้ว่า2πrเท่ากับ 360 °
2πr = 360 °
πr = 180 °
1r = 180 ° / π
r = 180 ° / 3.14 (ในฐานะπ = 3.14)
ดังนั้น 1r ≈ 57.295
สามารถใช้การแปลงระหว่างเรเดียนและองศา อย่างไรก็ตามตารางนี้สามารถช่วยในการแปลงที่พบบ่อยมากขึ้น
องศา | เรเดียน (แน่นอน) | เรเดียน (ประมาณ) |
30 ° | π / 6 | 0.524 |
45 ° | π / 4 | 0.785 |
60 ° | π / 3 | 1.047 |
90 ° | π / 2 | 1.571 |
180 องศา | π | 3.142 |
270 ° | 3π / 2 | 4.712 |
360 ° | 2π | 6.283 |
เปรียบเทียบระหว่างเรเดียนและระดับ:
เรเดียน | ระดับ | |
แบบเต็ม | เรเดียน | ระดับของส่วนโค้ง, ส่วนโค้งหรือส่วนโค้ง |
แบบสั้น | ราด | องศา |
สัญลักษณ์ | c ตัวยก | ° |
หน่วยของ | มุม | มุม |
ระบบหน่วย | หน่วย SI ที่ได้รับ | หน่วยที่ยอมรับ SI |
คำจำกัดความตาม Dictionary.com | การวัดของมุมศูนย์กลางที่รองรับอาร์คเท่ากับความยาวถึงรัศมี | ส่วนที่ 360 ของมุมที่สมบูรณ์หรือเลี้ยวโดยมักแสดงด้วยเครื่องหมาย°เช่นเดียวกับใน 45 °ซึ่งอ่านได้ที่ 45 องศา |
ลักษณะ | เรเดียนขึ้นอยู่กับรัศมีของวงกลม รัศมีของวงกลมคือเส้นใดก็ตามที่ลากในวงกลมที่เชื่อมต่อศูนย์กลางของวงกลมกับเส้นรอบวง เส้นนี้จะถูกถ่ายและวัดรอบเส้นรอบวงของวงกลมเมื่อจุดเริ่มต้นของเส้นและจุดสิ้นสุดของเส้นเชื่อมต่อกับจุดกึ่งกลางเส้นจะเกิดเป็นมุม มุมนี้เรียกว่าเรเดียน 1 อัน | แต่ละระดับแสดงถึง 1/360 ของการหมุนเต็ม ซึ่งหมายความว่าแต่ละวงกลมแบ่งออกเป็น 360 องศาและการเคลื่อนไหวแต่ละครั้งจะถูกนับเป็น 1 ° |
เท่ากัน | หนึ่ง rad เท่ากับ 57.295 องศา | หนึ่งองศาเทียบเท่ากับπ / 180 เรเดียน |