ความแตกต่างที่สำคัญ: วงกลมและวงรีมีรูปร่างโค้งปิด ในวงกลมจุดทั้งหมดอยู่ห่างจากจุดศูนย์กลางเท่ากันซึ่งไม่ใช่กรณีที่มีวงรี ในวงรีจุดทั้งหมดอยู่ในระยะทางที่แตกต่างจากจุดศูนย์กลาง
ในทางคณิตศาสตร์วงกลมเป็นรูปร่างที่สำคัญในเขตของรูปทรงเรขาคณิตและสถานะคำจำกัดความของมัน: วงกลมเป็นรูปทรงที่มีทุกจุดในระยะทางเดียวกันจากจุดศูนย์กลาง มันตั้งชื่อตามศูนย์กลางของมัน ตัวอย่างในโลกแห่งความเป็นจริงของวงกลมคือล้อจานอาหารเย็นและพื้นผิวเหรียญ
คำว่า ' ละครสัตว์ ' นั้นมาจากคำว่า ' kirkos ' ของกรีกซึ่งเป็นคำเปรียบเทียบของภาษาอเมริคกรีกและหมายถึง ' ห่วง ' หรือ ' แหวน ' วงกลมเป็นที่รู้จักกันก่อนประวัติศาสตร์ที่บันทึกไว้ ดวงอาทิตย์และดวงจันทร์เป็นตัวอย่างตามธรรมชาติของวงกลมในขณะที่แม้ก้านลมสั้น ๆ ที่พัดผ่านสายลมจะก่อรูปร่างเป็นวงกลมในทราย หลักการของวงกลมถูกนำไปใช้ในการก่อตัวของล้อและเกียร์โดยคนก่อนประวัติศาสตร์ ในยุคปัจจุบันมีเครื่องจักรมากมายหลายชนิดตามรูปร่างของวงกลม การศึกษาของวงกลมและการพัฒนานั้นมีผลบังคับใช้ในสาขาคณิตศาสตร์เรขาคณิตดาราศาสตร์และแคลคูลัส
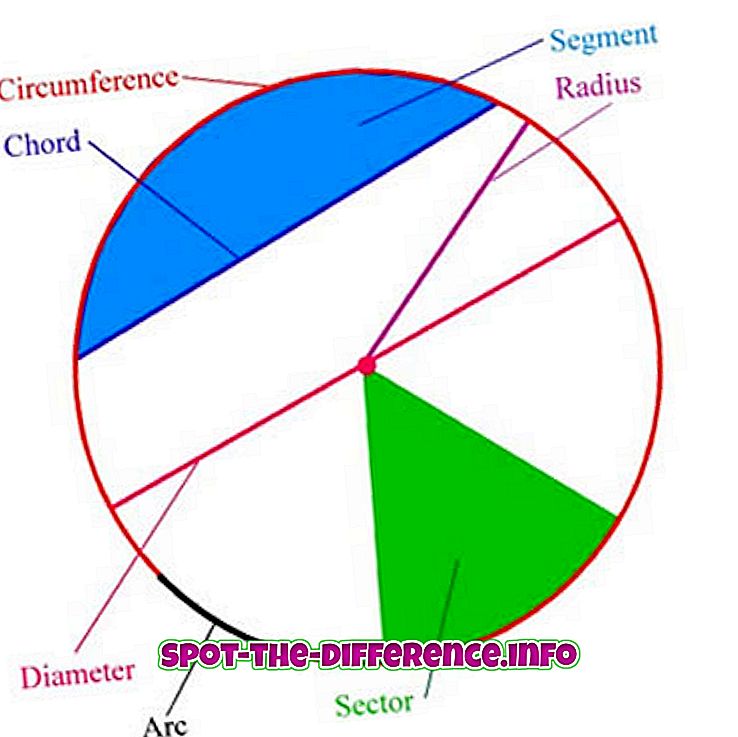
ข้อกำหนดต่อไปนี้เกี่ยวข้องกับคำศัพท์ของวงกลม:
Arc : ส่วนใดส่วนหนึ่งที่เชื่อมต่อของวงกลม
ศูนย์ : จุดที่มีระยะห่างจากจุดบนวงกลม
Radius : ส่วนของเส้นตรงที่รวมศูนย์กลางของวงกลมไปยังจุดใด ๆ บนวงกลมนั้น หรือความยาวของส่วนดังกล่าวซึ่งมีขนาดครึ่งเส้นผ่าศูนย์กลาง
เส้นผ่านศูนย์กลาง : ส่วนของเส้นตรงที่จุดปลายอยู่บนวงกลมและผ่านจุดกึ่งกลาง หรือความยาวของส่วนของเส้นตรงซึ่งเป็นระยะทางที่ใหญ่ที่สุดระหว่างจุดสองจุดใด ๆ บนวงกลม มันเป็นกรณีพิเศษของคอร์ดคือคอร์ดที่ยาวที่สุดและมันคือรัศมีสองเท่า
Circumferenc e: ความยาวของหนึ่งวงจรตามวงกลม
Chord : ส่วนของเส้นตรงที่จุดปลายอยู่บนวงกลม
แทนเจนต์ : เส้นตรง coplanar ที่สัมผัสวงกลมที่จุดเดียว
Semicircl e: บริเวณที่ล้อมรอบด้วยเส้นผ่านศูนย์กลางและส่วนโค้งอยู่ระหว่างจุดสิ้นสุดของเส้นผ่านศูนย์กลาง มันเป็นกรณีพิเศษของส่วนวงกลมคือส่วนที่ใหญ่ที่สุด
หนังสือเวียนเซกเตอร์ : ภูมิภาคล้อมรอบด้วยรัศมีสองและโค้งอยู่ระหว่างรัศมี
ในทางคณิตศาสตร์วงรีเป็นรูปร่างทั่วไปในสาขาคณิตศาสตร์ สถานะคำจำกัดความของมัน: เส้นโค้งที่สร้างวงปิดซึ่งผลรวมของระยะทางจากจุดสองจุด (foci) ไปยังทุกจุดบนเส้นนั้นคงที่ ตัวอย่างชีวิตจริงของวงรีคือ: ห่วงฮูลา, แก้วน้ำและจานอาหารค่ำที่เรียบง่ายเมื่อเอียงเพื่อดูในมุม
Apollonius of Perga ให้ชื่อ 'วงรี' ใน Conics ของเขาซึ่งเน้นการเชื่อมต่อของเส้นโค้งด้วยการใช้พื้นที่ มันเป็นเส้นโค้งบนระนาบที่ล้อมรอบจุดโฟกัสสองจุดซึ่งเส้นตรงที่ลากจากจุดโฟกัสจุดใดจุดหนึ่งไปยังจุดใด ๆ บนโค้งแล้วกลับไปยังจุดโฟกัสอื่นมีความยาวเท่ากันทุกจุดบนโค้ง รูปร่างของมันถูกแสดงด้วยความเยื้องศูนย์ซึ่งใกล้เคียงกับ 1 การศึกษาของวงรีและคุณสมบัติของมันนั้นมักจะใช้ในด้านฟิสิกส์ดาราศาสตร์และวิศวกรรม วงโคจรของดาวเคราะห์ที่มีดวงอาทิตย์ ณ จุดโฟกัสดวงจันทร์ดวงหนึ่งโคจรรอบดาวเคราะห์และระบบอื่นที่มีวัตถุทางดาราศาสตร์สองดวงเป็นตัวอย่างทั่วไปของเส้นทางรูปไข่ รูปทรงของดาวเคราะห์และดวงดาวนั้นมักจะถูกอธิบายโดยวงรี วงรีนั้นยังถือว่าเป็นรูป Lissajous ที่ง่ายที่สุดซึ่งเกิดขึ้นเมื่อการเคลื่อนไหวในแนวนอนและแนวตั้งเป็นไซนัสด้วยความถี่เดียวกัน
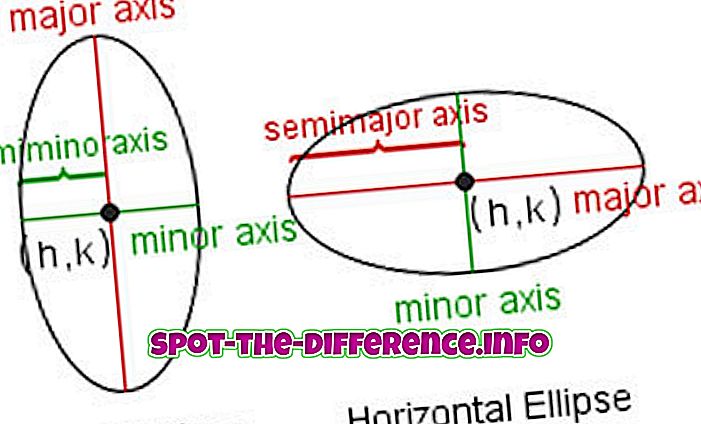
คำศัพท์ที่เกี่ยวข้องส่วนใหญ่ในคำศัพท์ของวงรีคือ:
โฟกัส : ระยะห่างจากศูนย์กลางและแสดงเป็นรัศมีหลักและรัศมีรอง
ความเยื้องศูนย์ : ความเยื้องศูนย์ของวงรี (โดยทั่วไปจะแทนด้วย e หรือε) แสดงด้วยการใช้ปัจจัยแฟบ
Directrix : มันเป็นเส้นคู่ขนานกับแกนเล็ก ๆ น้อย ๆ และเกี่ยวข้องกับการโฟกัสแต่ละครั้ง
Latus rectum : คอร์ดของวงรีที่ตั้งฉากกับแกนหลักและผ่านจุดโฟกัสจุดใดจุดหนึ่งเรียกว่า latus rectum ของวงรี
แกน Major / Minor : เส้นผ่านศูนย์กลางยาวที่สุดและสั้นที่สุดของวงรี ความยาวของแกนหลักเท่ากับผลรวมของเส้นกำเนิดสองเส้น
แกนกึ่งหลัก / กึ่งรอง : ระยะทางจากจุดศูนย์กลางไปยังจุดที่อยู่ไกลที่สุดและใกล้เคียงที่สุดบนวงรี ครึ่งแกนหลัก / รอง
คอร์ด : จุดกึ่งกลางของชุดคอร์ดคู่ขนานของวงรีคือ collinear
เส้นรอบวง : มันเกี่ยวข้องกับความยาวของแกนกึ่งหลักและความเยื้องศูนย์และเป็นส่วนหนึ่งของวงรี
การเปรียบเทียบระหว่าง Circle กับ Ellipse:
วงกลม | วงรี | |
คำนิยาม | วงกลมเป็นรูปวงกลมเครื่องบินที่มีขอบเขต (เส้นรอบวง) ประกอบด้วยจุดที่มีระยะเท่ากันจากจุดคงที่ (จุดศูนย์กลาง) | วงรีเป็นรูปวงรีปกติโดยมีจุดเคลื่อนที่ในระนาบเพื่อให้ผลรวมของระยะทางจากจุดอื่นสองจุด (จุดโฟกัส) คงที่หรือเป็นผลเมื่อกรวยถูกตัดด้วยระนาบเฉียง ไม่ตัดเส้น |
รูปแบบ | วงกลมไม่ได้มีรูปทรงแตกต่างกัน พวกเขายังคงรูปร่างเหมือนเดิมแม้ว่าจะเปลี่ยนมุมมอง | วงรีมีรูปร่างแตกต่างกันไปตั้งแต่วงกว้างและแบนจนถึงเกือบเป็นวงกลมขึ้นอยู่กับว่าจุดโฟกัสอยู่ห่างจากกันมากแค่ไหน |
ความสม่ำเสมอของรัศมี | มันมีรัศมีคงที่ตลอดทั้งรูปร่าง | มันไม่มีรัศมีคงที่ตลอดทั้งรูปร่าง |
องค์ประกอบหลัก | วงกลมมีรัศมีหนึ่งอันซึ่งอยู่ที่กึ่งกลาง | วงรีมีจุดโฟกัสสองจุดซึ่งอยู่ที่ปลายทั้งสองด้าน |
พื้นที่ | π × r ^ 2 ที่ 'r' คือรัศมีของวงกลม | π× a × b โดยที่ 'a' คือความยาวของแกนกึ่งหลักและ 'b' คือความยาวของแกนกึ่งรอง |
สมการมาตรฐาน | (xa) ^ 2 + (yb) ^ 2 = r ^ 2 | x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1 |
ความคล้ายคลึง | แวดวงเป็นรูปทรงที่เป็นเอกลักษณ์ซึ่งมีรูปร่างอื่นเกิดขึ้น | จุดไข่ปลาก็เกิดขึ้นเป็นภาพของวงกลมภายใต้การฉายแบบขนานและกรณีขอบเขตของการฉายมุมมอง |