ความแตกต่างหลัก: พาราโบลาเป็นส่วนรูปกรวยที่สร้างขึ้นเมื่อระนาบตัดพื้นผิวรูปกรวยขนานกับด้านข้างของกรวย ไฮเพอร์โบลาถูกสร้างขึ้นเมื่อระนาบตัดพื้นผิวรูปกรวยขนานกับแกน

Parabola และ hyperbola เป็นคำที่ต่างกันสองส่วนและสมการที่ใช้ในคณิตศาสตร์เพื่ออธิบายสองส่วนที่แตกต่างกันของรูปกรวย สิ่งเหล่านี้มีรูปร่างขนาดและปัจจัยอื่น ๆ ที่แตกต่างกันรวมถึงสูตรที่ใช้ในการคำนวณ เพื่อที่จะเข้าใจพวกเขาก่อนอื่นมาทำความเข้าใจกับกรวยและส่วนที่แตกต่างกันของรูปกรวย

ส่วนรูปกรวยคือส่วนโค้งที่ได้มาเมื่อระนาบตัดกับกรวยในรูปแบบต่าง ๆ การตัดที่ได้จากจุดตัด ได้แก่ วงรีวงกลมพาราโบลาและไฮเพอร์โบลา ตามรูปทรงเรขาคณิตของการวิเคราะห์รูปกรวยถูกกำหนดให้เป็น“ เส้นโค้งพีชคณิตระนาบของระดับ 2” คำจำกัดความที่ได้รับความนิยมของส่วนรูปกรวยรวมถึงจุดโฟกัสเส้น directrix และความเยื้องศูนย์ จุดโฟกัสและเส้น directrix นั้นคาดว่าจะมีการปันส่วนคงที่ในรูปกรวย อัตราส่วนนี้เป็นที่รู้จักกันในนามของส่วนรูปกรวย ความเยื้องศูนย์กลางของวงรีพาราโบลาและไฮเปอร์โบลาแตกต่างกัน ellipses มีความเยื้องศูนย์น้อยกว่า 1, parabolas มีความเยื้องศูนย์ที่เท่ากับ 1 และไฮเปอร์โบลามีความเยื้องศูนย์มากกว่า 1 งานที่รู้จักเร็วที่สุดในรูปกรวยสามารถย้อนกลับไปในศตวรรษที่สี่โดย Menaechmus ซึ่งค้นพบวิธี เพื่อแก้ปัญหาของการเสแสร้งลูกบาศก์ผ่านการใช้ Parabolae

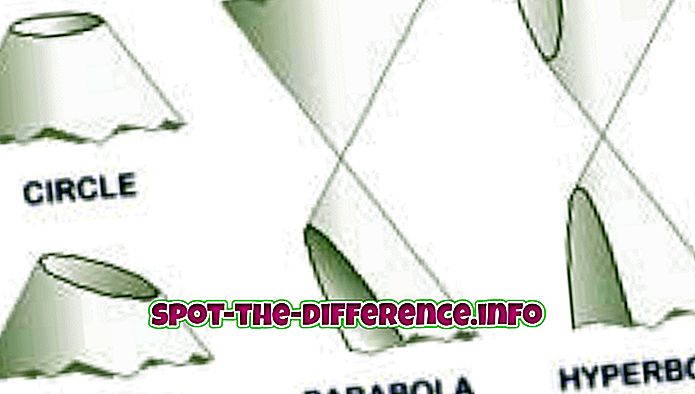
พาราโบลาเป็นส่วนรูปกรวยที่สร้างขึ้นเมื่อระนาบตัดกับกรวย Parabolae หรือ parabolas ก่อตัวขึ้น 'จากจุดตัดของพื้นผิวทรงกรวยขวาและระนาบขนานไปกับเส้นตรงที่สร้างพื้นผิวนั้น' อีกวิธีหนึ่งที่สร้างพาราโบลาคือเมื่อตำแหน่งของจุดบนระนาบที่มีระยะเท่ากันจากการโฟกัสและไดเรกทริกซ์จะสร้างพาราโบลา ในพีชคณิตพาราโบลามักถูกใช้ในกราฟของฟังก์ชันกำลังสองโดยใช้สูตร y = x ^ 2

เส้นที่แยกพาราโบลาผ่านกลางนั้นเป็นที่รู้จักกันในนามของแกนสมมาตร บรรทัดนี้ตั้งฉากกับทิศทางและผ่านการโฟกัส จุดที่อยู่บนแกนสมมาตรที่ตัดพาราโบลาเรียกว่า 'จุดยอด' ระยะห่างระหว่างจุดยอดและโฟกัสเป็นที่รู้จักกันในชื่อ 'ความยาวโฟกัส' Parabolas สามารถเปิดในทิศทางใดก็ได้รวมถึงขึ้นลงขวาหรือซ้าย คุณสมบัติหลักของพาราโบลาก็คือพวกมันเหมือนกันทุกขนาดเท่านั้น พวกเขาสามารถปรับตำแหน่งและลดขนาดให้พอดีกับพาราโบลาอื่น ๆ Parabolas ใช้ในแอปพลิเคชันต่าง ๆ เช่นตัวสะท้อนแสงไฟหน้ารถยนต์การออกแบบขีปนาวุธเป็นต้นพวกเขายังมีบทบาทสำคัญในฟิสิกส์วิศวกรรมคณิตศาสตร์และอื่น ๆ

ไฮเปอร์โบลาเป็นเส้นโค้งเรียบที่เกิดขึ้นเมื่อระนาบตัดกับกรวยที่ขนานกับแกน y ที่สร้างการตัดตามแนวด้านข้างของกรวย ไฮเพอร์โบลาถูกกำหนดโดยคุณสมบัติเชิงเรขาคณิตหรือสมการของมันซึ่งเป็นชุดการแก้ปัญหา คำว่า 'ไฮเพอร์โบลา' มาจากคำภาษากรีกซึ่งหมายถึง "การโยนมากเกินไป" หรือ "มากเกินไป" เชื่อว่าเป็นคำที่ประกาศเกียรติคุณจาก Apollonius ของ Perga ผู้มีส่วนร่วมอย่างมากในการศึกษาของส่วนที่มีรูปกรวย

ไฮเปอร์โบลาเป็นที่รู้จักกันว่ามีกิ่งที่เป็นภาพสะท้อนซึ่งกันและกันและมีลักษณะคล้ายกับคันธนูที่ไม่มีที่สิ้นสุด จุดบนกิ่งไม้สองกิ่งที่อยู่ใกล้กันเรียกว่าจุดยอด เส้นที่เชื่อมต่อจุดยอดนั้นเรียกว่าแกนขวางหรือแกนหลักซึ่งสอดคล้องกับเส้นผ่านศูนย์กลางหลักของวงรี จุดกึ่งกลางของแกนขวางเรียกว่าศูนย์กลางของไฮเพอร์โบลา สมการของไฮเพอร์โบลาเขียนเป็น x2 / a2- y2 / b2 = 1 ไฮเปอร์โบลาถูกใช้ในแอพพลิเคชั่นต่าง ๆ ในโลกปัจจุบันรวมถึงเส้นทางตามด้วยเงาของปลายนาฬิกาแดดรูปร่างของวงเปิด มันถูกใช้เป็นซุ้มประตูในอาคารที่สร้างขึ้นมากมายเช่นสมการทางคณิตศาสตร์และเรขาคณิตฟิสิกส์ ฯลฯ

ไฮเพอร์โบลาและพาราโบลาเป็นทั้งโค้งเปิดซึ่งหมายความว่าพวกมันไม่ได้จบและยังคงอยู่กับอินฟินิตี้อย่างไม่มีกำหนดสิ่งที่รีและวงกลมไม่สามารถทำได้