ความแตกต่างหลัก: จุดคือจุดที่หมายถึงตำแหน่งที่ถูกทำเครื่องหมายบนพื้นที่ไม่มีที่สิ้นสุดหรือพื้นผิวระนาบ เส้นนั้นถือเป็นมิติเดียวและได้รับการแนะนำให้รู้จักกับวัตถุที่เป็นเส้นตรงที่ไม่มีความกว้างและความลึก ระนาบเป็นพื้นผิวเรียบสองมิติที่มีขนาดใหญ่อย่างไม่มีกำหนดที่มีความหนาเป็นศูนย์
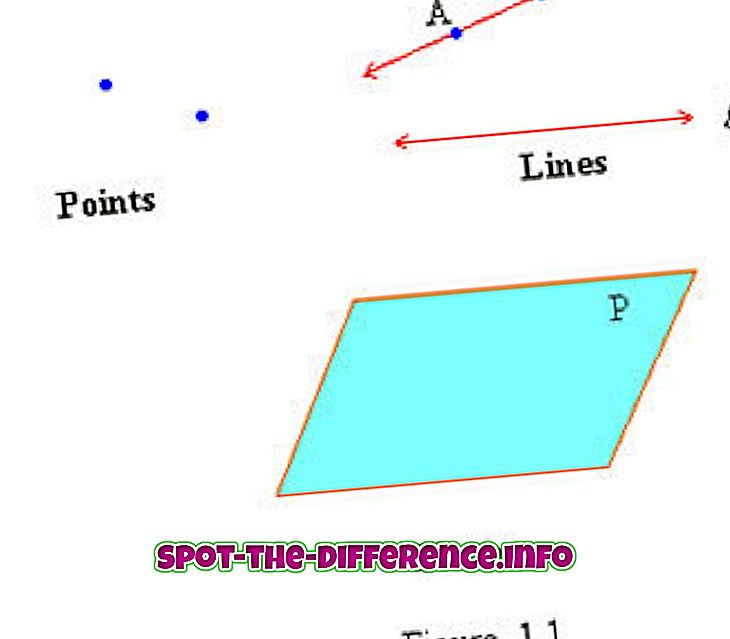
จุดเส้นและระนาบถือเป็นเงื่อนไขทางเรขาคณิตที่ไม่ได้กำหนดเนื่องจากไม่ได้กำหนดอย่างเป็นทางการ เมื่อเรากำหนดคำศัพท์มันมักจะใช้คำที่ง่ายกว่าในการอธิบายคำนั้น อย่างไรก็ตามจุดเส้นและระนาบถือเป็นคำศัพท์ที่ง่ายขึ้นแล้ว แนวคิดทางเรขาคณิตอื่น ๆ ทั้งหมดถูกสร้างขึ้นบนจุดเส้นและระนาบ อย่างไรก็ตามลองทำความเข้าใจกับคำศัพท์ทั้งสามที่ไม่ได้กำหนด
จุดคือจุดที่ไม่ได้หมายถึงสิ่งใดสิ่งหนึ่ง แต่แทนตำแหน่ง จุดแทนตำแหน่งที่ถูกทำเครื่องหมายในพื้นที่ไม่มีที่สิ้นสุดหรือบนพื้นผิวของระนาบ จุดสามารถเป็นจุดขนาดใดก็ได้ แต่ไม่มีความยาวความกว้างหรือความหนา นี่เป็นเพราะมันเป็นตัวแทนของสถานที่และไม่ใช่สิ่งที่
มีการตั้งชื่อคะแนนโดยใช้ตัวอักษรตัวพิมพ์ใหญ่เช่น A, B, C เป็นต้นในพื้นที่แบบยุคลิดแบบสองมิติที่รู้จักกันดีในชื่อกริดหรือกราฟที่มีแกน x และแกน y จุดจะถูกแทนด้วย สั่งคู่ (x, y) x แทนตำแหน่งแนวนอนของจุดในขณะที่ y แทนตำแหน่งแนวตั้ง มีจุดสองชุด: Collinear และ Coplanar ชุดของจุด Collinear อยู่ในแนวเส้นตรงในขณะที่ชุดเส้น Coplanar อยู่บนระนาบเดียวกัน
เส้นนั้นถือเป็นมิติเดียวและได้รับการแนะนำให้รู้จักกับวัตถุที่เป็นเส้นตรงที่ไม่มีความกว้างและความลึก คำจำกัดความของการเปลี่ยนแปลงของเส้นขึ้นอยู่กับประเภทของรูปทรงเรขาคณิต ในเรขาคณิตของยุคลิดเส้นไม่มีการกำหนดชุด ในเรขาคณิตวิเคราะห์เส้นในระนาบถูกกำหนดเป็นชุดของจุดที่พิกัดตรงกับสมการเชิงเส้นที่กำหนด ในเรขาคณิตเชิงอุบัติการณ์เส้นอาจเป็นวัตถุอิสระจากชุดของจุดที่อยู่บนมัน
สายได้รับการยอมรับว่าเป็นชุดจุดที่ไม่สิ้นสุดหนึ่งมิติที่เชื่อมต่อ เส้นตรงคือระยะทางที่สั้นที่สุดระหว่างสองจุดบนเครื่องบิน เส้นถูกทำเครื่องหมายด้วยลูกศรสองตัวที่ส่วนท้ายของแต่ละอันเพื่อบ่งบอกว่ามันไม่สิ้นสุด เส้นถูกตั้งชื่อในสองวิธี: สองจุดบนบรรทัดหรือโดยตัวอักษรตัวพิมพ์เล็กตัวเดียว จุดสองจุดใด ๆ ที่ทำเครื่องหมายไว้บนบรรทัดสามารถใช้เพื่ออ้างถึงบรรทัด ตัวอย่างเช่น: บรรทัดที่มีคะแนน H, I ที่มันจะมีข้อความบรรทัด HI และจะถูกวางไว้ด้านบนของมันเพื่อแสดงว่ามันเป็นเส้น
ระนาบเป็นพื้นผิวเรียบสองมิติที่มีขนาดใหญ่อย่างไม่มีกำหนดที่มีความหนาเป็นศูนย์ ระนาบถือเป็นอะนาล็อกสองมิติของจุด (ขนาดศูนย์), เส้น (หนึ่งมิติ) และของแข็ง (สามมิติ) เมื่อพิจารณาถึงคำจำกัดความในแง่ของพื้นที่ยูคลิด, เครื่องบินหมายถึงพื้นที่ทั้งหมด ลองจินตนาการถึงแผ่นโลหะที่ไม่มีความหนาอย่างไรก็ตามมันจะดำเนินต่อไปตลอดกาลและตลอดไป นั่นถือเป็นเครื่องบิน
Wikipedia กล่าวว่า“ งานพื้นฐานหลายอย่างในวิชาคณิตศาสตร์เรขาคณิตตรีโกณมิติทฤษฎีกราฟและการทำกราฟจะดำเนินการในพื้นที่สองมิติหรือกล่าวอีกนัยหนึ่งในระนาบ” แม้ว่าระนาบนั้นจะไม่มีที่สิ้นสุด ขอบ ระนาบเหล่านี้ถูกวาดโดยคู่ขนานสองคู่และดูเหมือนว่าเป็นสี่เหลี่ยมมุมฉาก เครื่องบินมีสองมิติ: ความยาวและความกว้าง แต่เนื่องจากเครื่องบินมีขนาดใหญ่มากความยาวและความกว้างจึงไม่สามารถวัดได้
เครื่องบินถูกกำหนดโดยสามคะแนน เครื่องบินมีสองประเภท: ระนาบขนานและระนาบตัดกัน ระนาบขนานเป็นระนาบสองลำขึ้นไปที่ไปเรื่อย ๆ โดยไม่ต้องข้ามเส้นทางของกันและกัน ลองนึกภาพแผ่นโลหะก่อนหน้านี้ตอนนี้เพิ่มแผ่นโลหะอื่นที่อยู่ด้านบนของมันและยังคงอยู่ตลอดไป ทั้งสองนี้จะสร้างระนาบคู่ขนานที่ไม่เคยตัดกัน อย่างไรก็ตามเครื่องบินที่น่าสนใจอยู่ตรงนั้น นี่คือเครื่องบินสองลำที่ข้ามเส้นทางของกันและกัน โดยทั่วไปเครื่องบินจะถูกตั้งชื่อด้วยอักษรตัวใหญ่ตัวพิมพ์ใหญ่เดียวที่เขียนด้วยตัวสะกด (Plane P)
ในเรขาคณิตจุดเส้นและระนาบจะรวมอยู่ในรูปแบบของการวางตัว สมมุติฐานนี้เป็นชุดของสมมติฐานสามประการ (สัจพจน์) ที่สามารถใช้เป็นส่วนหนึ่งของพื้นฐานสำหรับเรขาคณิตแบบยุคลิดในสามมิติหรือมากกว่านั้น สมมติฐานที่สามประกอบด้วย: สมมติฐานของบรรทัดที่ไม่ซ้ำสมมติฐานของหมายเลข ข้อสันนิษฐานของบรรทัดที่ไม่ซ้ำกันแสดงให้เห็นว่ามีหนึ่งบรรทัดผ่านสองจุดที่แตกต่างกัน การสันนิษฐานว่าจำนวนบรรทัดทุกบรรทัดเป็นชุดของจุดที่สามารถใส่ลงในการติดต่อแบบหนึ่งต่อหนึ่งกับตัวเลขจริง จุดใด ๆ ที่สามารถสอดคล้องกับ 0 (ศูนย์) และจุดอื่น ๆ ที่สามารถสอดคล้องกับ 1 (หนึ่ง) ในที่สุดสมมติฐานมิติระบุรัฐที่กำหนดให้เส้นในระนาบมีอย่างน้อยหนึ่งจุดในระนาบที่ไม่ได้อยู่ในบรรทัด เมื่อพิจารณาจากระนาบในอวกาศมีจุดอย่างน้อยหนึ่งจุดที่ไม่ได้อยู่ในระนาบ